Calculatrice d’Intérêts Composés | Simulateur Tableau

Vous avez sûrement déjà entendu parler du fameux « pouvoir des intérêts composés » . Mais qu’est-ce donc concrètement ?
La notion d’intérêts composés, exprimée telle quelle, a de quoi paraître complexe. Pourtant, elle n’est pas si difficile à appréhender. Il s’agit de surcroît d’un principe essentiel à l’investisseur, et potentiellement du plus puissant catalyseur de votre patrimoine.
Tout investisseur de long terme devrait en effet mettre en place une stratégie lui assurant de bénéficier de l’impact des intérêts composés. Suivez le guide !

Calculateur de tableau d’intérêts composés
📚 Les autres simulateurs qui pourront vous être utiles :
- Simulateur de prêt immobilier,
- Simulateur de taux d’endettement,
- Simulateur en ligne : acheter ou louer.
Définition des intérêts composés
Le principe des intérêts composés consiste à calculer des intérêts non seulement sur le capital initial investi, mais aussi sur les intérêts accumulés au fil des périodes. Autrement dit, les intérêts générés chaque période sont ajoutés au capital pour calculer les intérêts de la période suivante. Cela permet à l’investissement de croître plus rapidement que les intérêts simples, où les intérêts sont calculés uniquement sur le capital initial.
Voici un exemple en graphique :
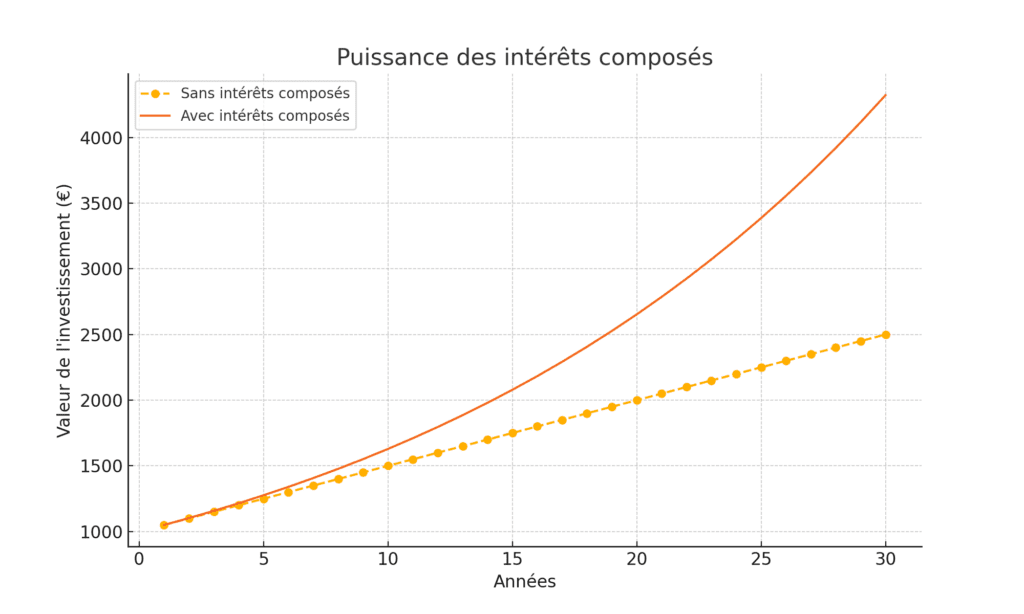
Cela peut paraître anodin, mais il s’agit d’un concept extrêmement puissant, puisque sur le long terme, les intérêts crédités, réinvestis encore et encore, produisent des rendements exponentiels.
Les exemples d’encensement des intérêts composés par nos illustres prédécesseurs sont légion. Albert Einstein déclarait à leur sujet qu’il s’agissait certainement de la plus grande force de l’univers.
On pourrait également citer celui qu’on surnomme l’oracle d’Omaha, et qui n’est autre que Warren Buffet. Buffet est considéré par le consensus comme un des plus grands investisseurs de l’histoire, et fut un temps « l’homme le plus riche du monde » selon le classement Forbes de 2008. Au sujet des intérêts composés, Buffet déclare : « Ma richesse vient essentiellement de la combinaison de trois choses : vivre en Amérique, la chance et les intérêts composés ».
Si l’on s’abstiendra de vous prodiguer des conseils sur votre lieu de résidence, ou sur d’éventuelles techniques pour booster votre chance, on ne peut en revanche que vous conseiller fortement le recours aux intérêts composés pour faire prospérer votre patrimoine.
Le fonctionnent des intérêts composés
Imaginons un exemple : vous épargnez 2 000 € par an sur un compte non rémunéré. Au bout de 10 ans, vous aurez épargné 20 000 €.
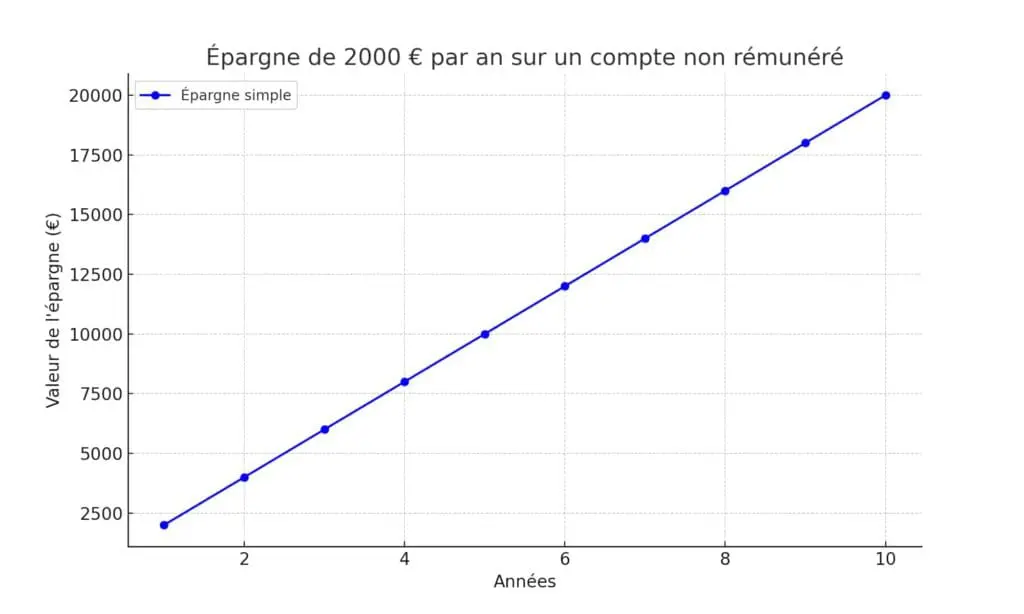
Deuxième exemple à présent : vous placez plutôt ces 2 000 € sur un portefeuille dont le taux d’intérêt est de 10% composé annuellement, ce qui signifie que la rémunération de votre capital s’y ajoute à chaque fin d’année. Les intérêts perçus sont donc réinvestis.
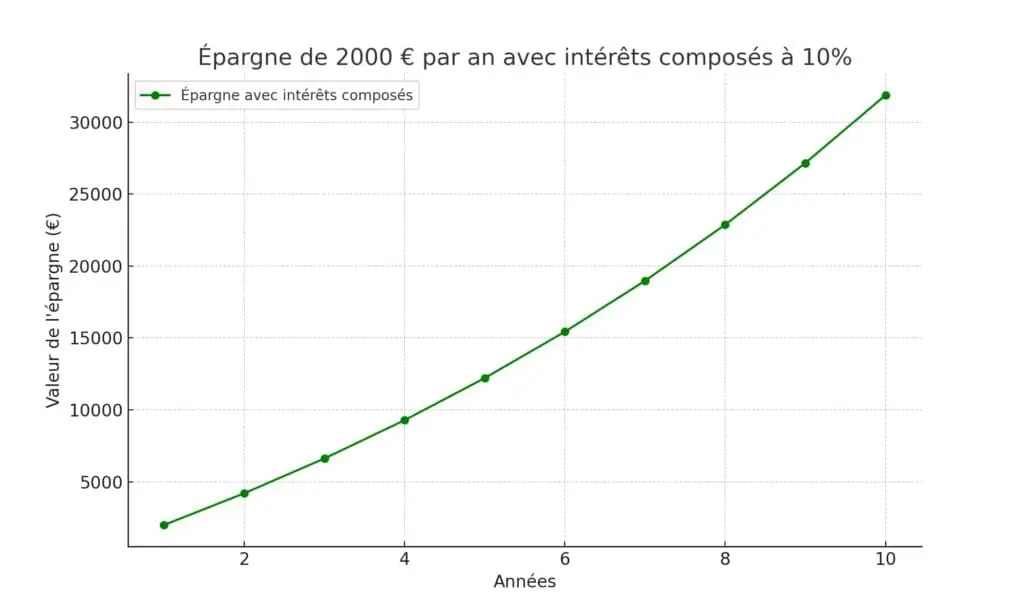
Étudions l’évolution de ce placement à travers un tableau :
| Année | Solde au 1er janvier | Explications |
|---|---|---|
| 1 | 2 000 € | Solde initial |
| 2 | 4 200 € | 2 000 € de l’année 1, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 3 | 6620 € | 4 200 € de l’année 2, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 4 | 9 282 € | 6620 € de l’année 3, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 5 | 12 210,20 € | 9 282 € de l’année 4, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 6 | 15 431,22 € | 12 210,20 € de l’année 5, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 7 | 18 974,34 € | 15 431,22 € de l’année 6, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 8 | 22 871,77 € | 18 974,34 € de l’année 7, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 9 | 27 158,95 € | 22 871,77 € de l’année 8, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| 10 | 31 874,85 € | 27 158,95 € de l’année 9, + 10% d’intérêts + 2 000 € nouvellement injectés. |
| Solde final | 35 062,33 € | 31 874,85 € de l’année 10, + 10% d’intérêts |
À travers ce tableau, l’on constate en un coup d’œil toute la puissance des intérêts composés. En effet, vous avez fait le même effort d’épargne dans les deux exemples. Cela vous aura couté précisément 20 000 € à chaque fois.
Mais dans le premier cas, le compte d’épargne non rémunéré, vous obtenez 20 000 € au bout de 10 années d’épargne. Dans le second cas, avec le même investissement, vous obtenez un solde de 35 062,33 €, soit plus de 15 000 € de différence !
💡 Cet exemple ne se base que sur une période de 10 ans ! Imaginez donc ce qu’il est possible de cumuler à plus long terme, avec des plus-values de plus en plus conséquentes, grâce au pouvoir exponentiel des intérêts composés !
Intérêts simples et intérêts composés : quelles différences ?
Même si dans la pratique, les produits proposant des intérêts simples ne sont pas courants, il est important de bien savoir distinguer les deux notions.
Concrètement, les intérêts simples ne sont calculés que sur votre capital placé. Ils sont donc fixes.
Par exemple, imaginons que vous placiez 1 000 € sur un produit financier dont le rendement est de 10% annuels, versé par intérêts simples. Vous gagnerez 100 € par an, soit les 10% d’intérêts, mais ceux-ci ne seront pas incorporés au capital pour le calcul de l’intérêt de l’année suivante. Vous toucherez simplement 100 €, tous les ans.
Dans la même situation, s’il s’agissait d’intérêts composés, vous auriez touché 100 € la première année, qui auraient été incorporés au capital pour le calcul des intérêts de la deuxième année. Ainsi, vos 10% de la deuxième année auraient été calculés sur une assiette de 1 100 €, et non pas 1 000 €. Vous auriez donc gagné 110 € pour cette deuxième année, ce qui aurait porté votre capital à 1 210 € pour le calcul du rendement de la troisième année. Et ainsi de suite…
Voici un graphique afin d’illustrer cet exemple :

On voit ici en un simple coup d’œil la différence de performance entre les intérêts simples et les intérêts composés. Ces derniers (en vert sur le graphique), réinvestis chaque année, augmentent l’assiette de calcul. Les intérêts générés sont de plus en plus conséquents au fil du temps, et ce de manière exponentielle. L’intérêt simple (en orange) est lui fixe, ne permettant qu’une croissance linéaire de l’investissement.
C’est véritablement l’effet « boule de neige » décrit à de nombreuses reprises par Warren Buffet et tous les grands investisseurs, une des forces les plus puissantes en gestion de patrimoine.
Il faut cependant distinguer les différents types d’intérêts composés.
Les différents types d’intérêts composés
Tous les types d’intérêts composés reposent sur le même principe, tel que décrit dans les exemples précédents.
Ce qui constitue leur spécificité réside dans la fréquence de capitalisation, c’est-à-dire, la périodicité à laquelle sont crédités les intérêts. Puisque ceux-ci sont réinvestis, et donc capitalisés, la fréquence à laquelle ils sont octroyés influence grandement la performance de l’investissement puisque, comme vu précédemment, c’est sur le long terme que se ressent le mieux l’effet « boule de neige » des intérêts composés.
Les intérêts simples
Avant d’étudier les différentes fréquences de capitalisation, rappelons ce que sont les intérêts simples. Comme évoqué plus haut, les intérêts simples sont une rémunération du capital, qui ne prend pas en compte les intérêts déjà versés dans le calcul des intérêts à venir. En somme, l’intérêt reste fixe, et la progression de l’investissement est linéaire.
Ex: vous placez 1 000 € sur un compte rémunéré à 5% (d’intérêts simples) le jour de vos dix-huit ans. Lorsque vous aurez trente ans, ce compte aura encaissé 12 fois les intérêts simples de 50 € (5%), et présentera un solde total de 1 600 €.
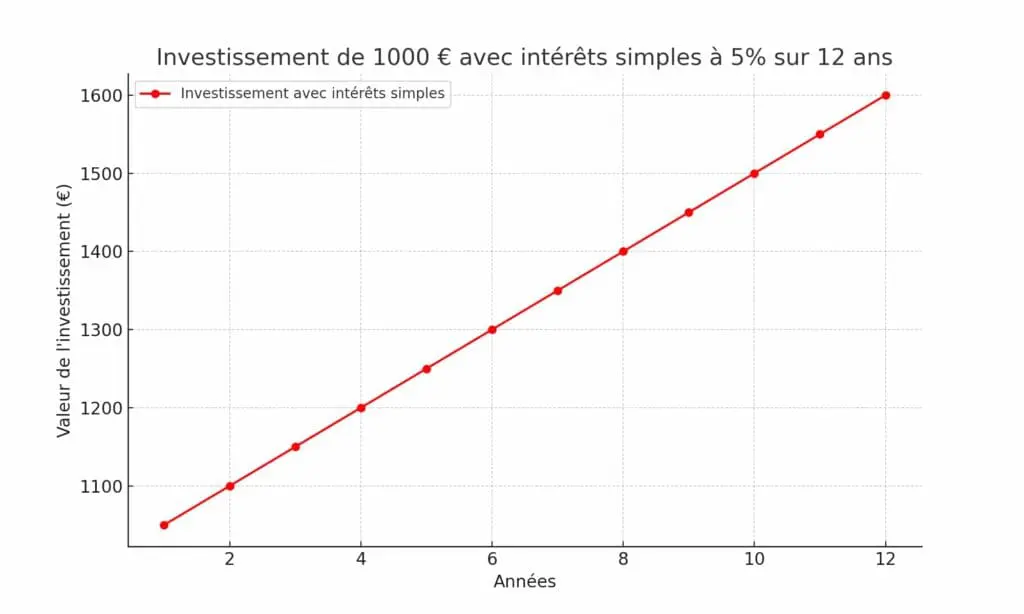
En comparaison avec les intérêts composés, les intérêts simples sont moins performants dans le temps, et ne présentent donc pas de réel intérêt en matière d’investissement (comparativement aux intérêts composés).
Les intérêts composés annuellement
L’intérêt composé annuellement est une forme d’intérêts composés, qui vise à rémunérer le capital et les intérêts déjà versés, afin de produire des « intérêts d’intérêts », de manière annuelle (ledit intérêt est donc versé une fois par an). Avec les intérêts composés annuellement, la performance du placement est exponentielle, puisque la rémunération versée est chaque année plus importante.
Exemple : reprenons le cas décrit pour les intérêts simples.
Vous placez 1 000 € sur un compte pour vos dix-huit ans, rémunérés à un taux d’intérêt composé annuellement de 5%. Chaque année, vous toucherez donc 5% du capital et des intérêts déjà versés. Au bout de 12 ans, soit à l’âge de trente ans, votre capital s’élève à 1 795,86 €.
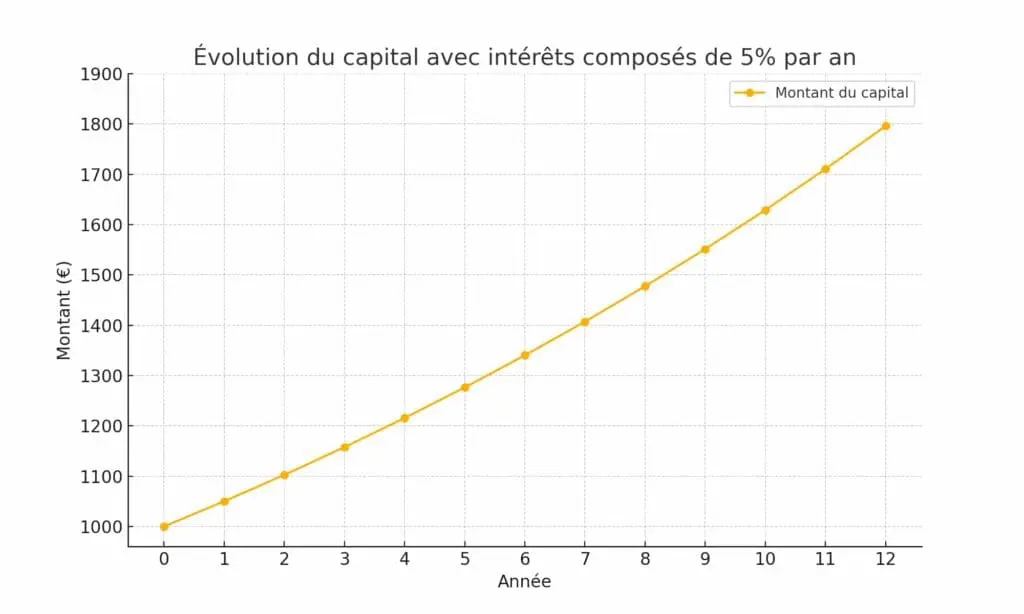
On parle beaucoup de livrets et de produits financiers qui versent des intérêts, mais la logique des intérêts composés s’applique également aux autres types d’investissement tels que le placement en bourse.
Avec les actions, les performances annuelles impactent le capital de départ, mais également les performances des années passées, qui étaient déjà venues gonfler ledit capital. Plus d’information dans notre guide dédié à l’achat d’actions.
Il en va de même avec les dividendes. L’on évoque souvent le réinvestissement des dividendes en action de la société émettrice, puisqu’un dividende réinvesti depuis 10 ans a généré des gains annuels à dix reprises, le principe même des intérêts composés. Tout cela, bien entendu, à condition de miser sur la bonne action. Pour cela, consultez notre sélections des meilleures actions à dividende.
Les intérêts composés comportent donc de nombreux avantages, mais également des aspects appelant à la vigilance.
✅ Les avantages des intérêts composés annuellement :
- Très performant sur le long terme, le temps joue en votre faveur,
- Encourage à garder son argent placé, puisque le gain généré est de plus en plus important,
- Applicable à une grande quantité d’actifs.
❌ Les inconvénients des intérêts composés annuellement :
- Peut s’avérer coûteux en frais si le montant initial des frais n’est pas avantageux (frais calculés sur des montants de plus en plus conséquents) ;
Les intérêts composés mensuellement
Les intérêts composés mensuellement fonctionnent exactement de la même manière que les intérêts composés annuellement. Leur méthode de calcul est strictement la même, seule la fréquence de capitalisation change.
Attention cependant, à bien se souvenir de la nature composée de ces intérêts mensuels. En effet nous pourrions être tenté de croire qu’un intérêt composé annuel de 12% équivaut à un intérêt composé mensuel de 1%, en faisant le raccourci : 1%, douze fois, est égal à 12%. C’est totalement faux.
En effet, imaginons que votre placement composé, à 1% mensuel, débute au 1er janvier. Le 31 janvier, vous toucherez vos 1% d’intérêt, qui seront pris en considération dans le calcul pour l’intérêt du mois de février, et tous les mois suivants, comme tout intérêt composé. À la fin de l’année, votre gain total sera donc plus avantageux qu’un placement à intérêt composé annuel de 12% !
Voici le graphique comparant les intérêts composés mensuellement et annuellement pour un investissement initial de 1 000 € à un taux annuel de 12%.
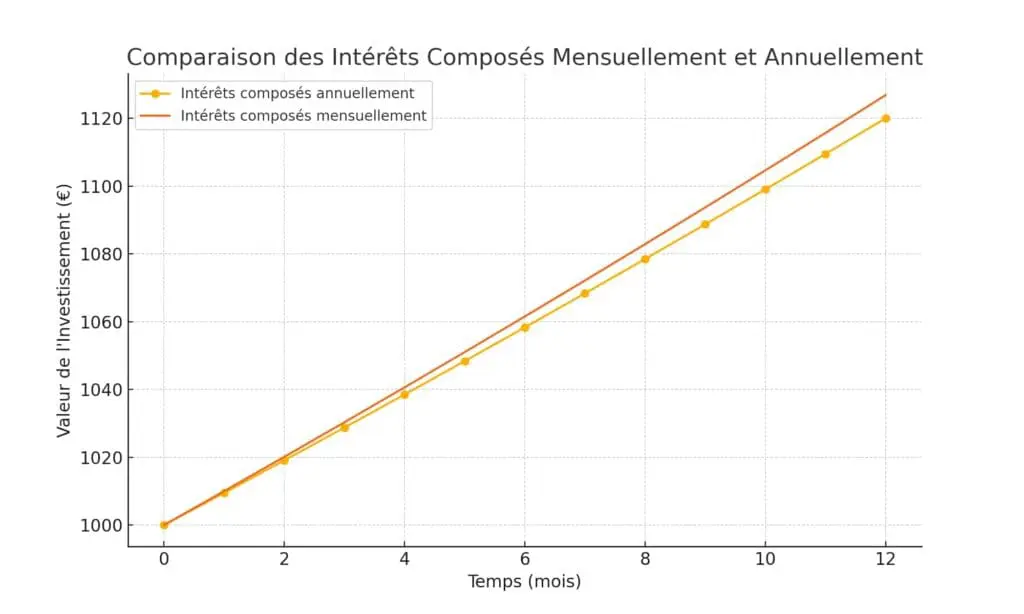
Le graphique illustre clairement que l’investissement avec intérêts composés mensuellement croît plus rapidement que celui avec intérêts composés annuellement.
Les avantages et inconvénients de l’intérêt composé mensuellement sont les mêmes que ceux de l’intérêt composé annuellement, à la différence près que le mensuel est encore plus avantageux puisque sa fréquence de capitalisation est plus élevée.
Intérêts composés continus
Les intérêts continus, ou composition continue, sont plus difficiles à appréhender, tant de manière pratique que mathématique. Nous n’entrerons pas ici dans la complexité logarithmique d’une telle notion.
Mais en résumé, la composition continue a pour objectif d’augmenter la période de capitalisation à l’infini, de manière à capitaliser en continu.
Ce type de capitalisation suppose donc de réinvestir les intérêts à chaque seconde, voire à chaque millième de seconde, voire encore sur une unité de temps plus petite.
Il s’agit donc du type d’intérêts composés le plus performant, car on le rappelle, plus le nombre de périodes de capitalisation est important, plus les intérêts générés sont conséquents.
Les avantages de ce mécanisme sont les mêmes que ceux des intérêts composés précédemment cités, même si l’on notera une rentabilité supérieure de la composition continue.
Le seul inconvénient de ce système est qu’il n’existe que très peu d’actifs, et de contextes, pour lesquels la mise en place de la composition continue est possible à long terme. Les actions peuvent correspondre à cette notion, à condition de sélectionner celles qui performent sur une période suffisante pour générer des rendements composés satisfaisants.
Comment calculer les intérêts composés ?
Calculer des intérêts composés est relativement simple et il existe plusieurs méthodes pour ce faire.
La formule universelle
La plus simple des méthodes consiste à utiliser la formule des intérêts composés :
V = C x (1+r)^n
Avec :
- V est la valeur future de l’investissement, c’est ce que l’on cherche à déterminer lorsque l’on dit, par exemple : « si je place 10 000 € à 6% d’intérêts composés annuellement, combien obtiendrai-je dans 10 ans ? »
- C est le capital de départ, soit dans notre exemple, 10 000 €
- r est le taux d’intérêt. S’il est de 5%, on écrira 0,05. Dans notre exemple, l’intérêt est de 6%, on écrira donc 0,06.
- n est le nombre de périodes de capitalisation, dans notre cas 10, pour 10 années. Pour un placement sur une autre durée de temps, par exemple, d’un an et demi, rémunéré en intérêts composés mensuellement, « n » équivaut à 18, car la composition est exprimée en mois, et un an et demi équivaut à 18 mois.
Appliquons à présent ce calcul à notre exemple (10 000 € à 6% composés annuellement, sur 10 ans) :
V = 10 000 x (1+0,06)^10
Soit V = 17 908,50 €
Le solde total de l’investissement sera, après 10 ans, de 17 908,50 €, soit une plus-value de 7 908,50 €, ou 79,085%.
Voici ce que cela donne :
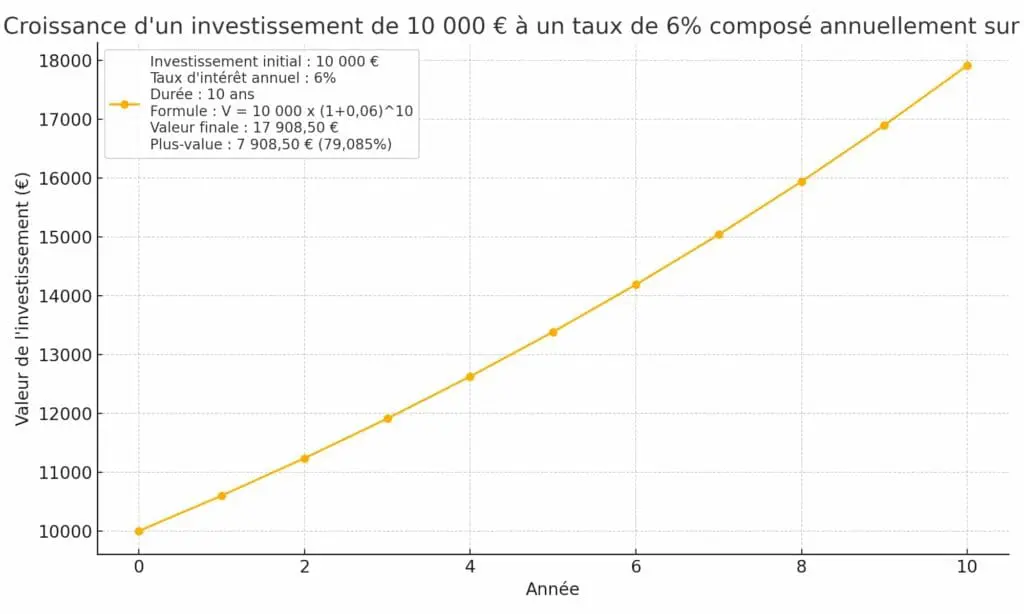
Il existe de nombreux outils en ligne qui appliquent cette méthode afin de vous permettre d’estimer vos rendements, mais il est important de comprendre le mécanisme, et de s’habituer à faire ses propres simulations afin de se rendre pleinement compte de la puissance des intérêts composés.
La « méthode 72 »
Cette méthode n’a pas pour objectif de déterminer le rendement d’un capital, mais d’estimer la durée nécessaire à atteindre un seuil symbolique en investissement : le doublement du capital.
À noter cette formule ne fait pas état d’une précision mathématique absolue, mais elle constitue un bon outil d’approximation qui peut aider à jauger rapidement une éventuelle décision d’investissement.
La formule se présente ainsi :
T = 72 / r
Avec :
- T est le temps, exprimé en périodes.
Attention: T n’est pas obligatoirement exprimé en nombre d’années. T dépend de chaque situation. Si votre intérêt est composé mensuellement, alors T est un nombre de mois. S’il l’est annuellement, il s’agit d’un nombre d’années. Par exemple, lorsque je dis : « Combien de temps me faudra-t-il pour faire doubler mon investissement de 10 000 €, dont l’intérêt composé annuel est de 7% ? », je cherche un nombre d’années. - r est le taux d’intérêt.
Appliquons à présent ce calcul à notre exemple (10 000 € à 7% composés annuellement) :
T = 72 / 7
Soit T = 10,28.
En d’autres termes, il me faudra 10,28 années pour faire doubler mon capital de 10 000 € et disposer de 20 000 € au total. En pratique, l’intérêt composé annuellement est généralement versé en fin d’année, et je disposerai donc de cette somme à la fin de la dixième année, soit au bout de 11 ans (pour tout produit de placement « non liquide »).
Les avantages et inconvénients des intérêts composés
Nous vous évoquions, en début d’article, la citation d’Albert Einstein au sujet des intérêts composés.
Mais il ne s’agissait pas de la seule citation attribuée à celui que l’on considère comme l’un des plus grands cerveaux du 20e siècle sur ce point.
Einstein aurait déclaré que « les intérêts composés sont la huitième merveille du monde. Celui qui le comprend s’enrichit ; celui qui ne le comprend pas le paie ».
Si la plupart des merveilles du monde ont disparu, les intérêts composés ont encore de beaux jours devant eux. En témoignent les ouvrages sur l’investissement, qui y font tous référence.
Récapitulons donc les avantages et inconvénients de cette méthode d’investissement, ou plutôt de cette notion, qui peut s’appliquer à de nombreuses stratégies d’investissement.
Avantages des intérêts composés
- Croissance rapide du capital : En fonction du taux d’intérêt composé, les débuts peuvent être longs. Une fois les premières périodes passées, la partie haute de l’exponentielle propre aux intérêts composés récompense l’investisseur patient.
- Potentiel de rendement élevé à long terme : Plus vous conserverez votre investissement, plus vous serez en mesure de goûter au réel potentiel des intérêts composés.
- Réinvestissement des intérêts : La composition des intérêts permet l’effet « boule de neige ». L’investisseur qui laisse ses intérêts « faire des petits » ne le regrette jamais.
- Économie de temps et d’efforts : Les intérêts composés permettent de gagner beaucoup de temps. Il suffit de réinvestir les intérêts lorsque cela n’est pas automatique.
- Flexibilité dans les choix d’investissement : De nombreux supports, comptes, et actifs permettent une stratégie « intérêts composés ». Pour les actifs à risques, attention à faire le bon choix. La logique “intérêts composés” est applicable aux actions, cryptomonnaies, OPCVM, etc.
Inconvénients des intérêts composés
- Horizon d’investissement : si vous êtes un investisseur court-termiste, adepte d’achats-reventes rapides, le principe des intérêts composés n’est pas fait pour vous.
- Possibilité de perte de capital : en fonction des actifs choisis et de votre appétence au risque, vous pouvez subir des pertes en capital. Si cela intervient en début d’investissement et impacte votre capital de départ, cela peut compromettre les chances de succès de votre stratégie d’intérêts composés.
- Risque d’inflation : il convient de toujours considérer l’inflation lorsque l’on se lance dans un investissement. Si votre taux d’intérêt composé est fixe, il faudra estimer ses chances de rester supérieur à l’inflation.
- Nécessité de planification financière rigoureuse : la puissance des intérêts composés est plus évidente à long terme, il convient de bien réfléchir au capital engagé et s’abstenir d’effectuer des retraits. On investit de l’argent que l’on peut perdre !
En conclusion, si vous n’aviez jamais entendu parler des intérêts composés avant de lire cet article, c’est chose faite. Tout investisseur désireux de faire fructifier son patrimoine à long terme doit s’intéresser aux intérêts composés car chacun peut l’appliquer à tout ou partie de son épargne, et observer la magie opérer.
Questions fréquentes sur les intérêts composés
Qu’est-ce que l’intérêt composé ?
L’intérêt composé est une notion permettant de faire croitre rapidement son patrimoine au fil des années.
Comment fonctionnent les intérêts composés ?
Les intérêts composés fonctionnent grâce à la participation des gains passés, aux gains futurs.
Quelle est la différence entre les intérêts simples et les intérêts composés ?
Les intérêts simples sont moins performants que les intérêts composés, car leur champ d’application n’est pas calculé sur la même base. N’étant pas réinvestis pour devenir partie du capital, ils ne produisent pas eux-même d’intérêts.
Quels sont les avantages et inconvénients des intérêts composés ?
Les intérêts composés présentent de nombreux avantages et inconvénients, mais ils peuvent néanmoins convenir à une majorité d’investisseurs. Pour plus d’informations, n’hésitez pas à consulter notre page dédiée.

MoneyRadar est composé de spécialistes de la finance et de la gestion de patrimoine qui ont pour mission d’accompagner les français dans leur éducation financière. Notre objectif est de rendre la finance accessible à tous, transparente et sans détours. Sur notre site, vous trouverez toutes les informations et avis d’experts pour vous aider à investir de manière éclairée.


